Teori Bilangan
3.1. Keterbagian
Kita telah mengetahui bahwa 13 dibagi 5 hasil baginya 2 dan sisanya 3 dan ditulis sebagai :
Secara umum, apabila a
bilangan bulat dan b bilangan bulat positif, maka ada tepat satu
bilangan bulat q dan r sedemikian hingga :
a = qb + r , 0 < r < b
dalam hal ini, q disebut
hasil bagi dan r sisa pada pembagian “a dibagi dengan b”. Jika r = 0
maka dikatakan a habis dibagi b dan ditulis b|a. Untuk a tidak habis
dibagi b ditulis b ditulis b ł a.
Sifat-sifat keterbagian :
-
a|b dan b|c maka a|c
-
ab|c maka a|c dan b|c
-
a|b dan a|c maka a|(bx + cy) untuk sembarang bilangan bulat x dan y.
Di sini akan dibuktikan sifat (1). Pembuktian sifat (2) dan (3) diserahkan kepada pembaca.
Bukti sisfat (1)
a|b maka b = ka
b|c maka c = lb = l (kl)a maka a|c.
Di bawah ini adalah kaidah-kaidah menentukan keterbagian suatu bilangan yang cukup besar.
-
Keterbagian oleh 2″
Suatu bilangan habis dibagi 2n jika n bilangan terakhir dari bilangan tersebut habis dibagi 2n.A1. Untuk n = 1 berarti suatu bilangan habis dibagi 2 jika angka terakhir dari bilangan tersebut habis dibagi 2.A2. Untuk n = 2 berarti suatu bilangan habis dibagi 4 jika 2 bilangan terakhir dari bilangan tersebut habis dibagi 4A3. Untuk n = 3 berarti suatu bilangan habis dibagi 8 jika 3 bilangan terakhir dari bilangan tersebut habis dibagi 8.Yang akan dibuktikan di sini adalah kaidah A1. Pembuktian kaidah A2 dan A3 diserahkan kepada pembaca.
Bukti kaidah A1
Misalkan bilangan itu :
a = …a3 a2 a1 a0
= 10(a3 a2 a1) + a0
Karena 10 (….a3 a2 a1) habis dibagi 2 maka agar a habis dibagi 2 maka haruslah a0 habis dibagi 2.
Contoh soal 1
Tentukan apakah 173332 habis dibagi oleh :
a). 2 b). 4 c). 8
pembuktian :
a). Karena 2|2 maka 2|173332
b). Karena 4|32 maka 4|173332
c). Karena 8 ł 332 maka 8 ł 173332
-
Keterbagian 3, 9, dan 11
Misalkan bilangan yang akan dibagi adalah a = an an-1 an-2 … a1 a0.B1. Bilangan a habis dibagi 3 jika jumlah angka-angkanya (an + an-1 + … + a1 + a0) habis dibagi 3B2. Bilangan a habis dibagi 9 jika jumlah angka-nagkanya (an + an-1 + … + a1 + a0) habis dibagi 9B3. Bilangan a habis dibagi 11 jika jumlah silang tanda ganti angka-angkanya (an – an-1 + an-2 + … ) habis dibagi 11Yang akan dibuktikan di sini adalah kaidah B1. Pembuktian kaidah B2 dan B3 diserahkan kepada pembaca.
Bukti kaidah B1.
a = an an-1 … a1 a0
= an X 10n + an-1 X 10n-1 + … + a1 X 10 + a0 X 100
= an X (9 + 1)n + an-1 X (9 + 1)n-1 + … + a1 X (9 + 1) + a0
= an[9n + n . 9n-1 + ... + 9n] + an + an-1 [9n-1 + (n-1)9n-2 + ... + 9(n-1)] + an-1 + … + 9a1 + a1 + a0
Dapat dipilih menjadi
dua bagian. Bagian pertama adalah jumlah semua suku yang merupakan
kelipatan 9 yang dilambangkan sebagai K(a) dan bagian kedua adalah
jumlah angka-angka :
Q(a) = an + an-1 + …
+ a1 + a0
+ a1 + a0
Maka : a = K(a) + Q(a)
Karena 3 | K(a) maka agar 3|a haruslah 3 | Q(a)
Contoh soal 2
Tentukan apakah 1815 habis dibagi :
a). 3 b). 9 c). 11
penyelesaian :
jumlah angka-angka 1815 = 1 + 8 + 1 + 5 = 15
a). Karena 3|15 maka 3|1815
b). Karena 9 ł 15 maka 9 ł 1815
c). Jumlah-silang tanda-ganti angka-angka bilangan 1815 = 1 – 8 + 1 – 5 = -11
Karena 11|-11 maka 11|1915
Contoh soal 3
Bilangan berangka enam berikut a1989b habis dibagi 72. Tentukan a dan b
Penyelesaian :
72 = 8 x 9. Karena itu 8|a1989b b = 6
Juga 9|a + 1 + 9 + 8 + 9 + b = a = 33 a = 3
-
BILANGAN KHUSUS
Di pasal ini, kita akan membahas beberapa bilangan khusus yakni bilangan prima, bilangan komposist dan bilangan kuadrat.
-
Bilangan Prima dan Komposit
Bilangan prima adalah bilangan asli yang hanya dapat dibagi oleh bilangan itu sendiri dan satu. Dengan perkataan lain, bilangan prima hanya mempunyai dua faktor. Misalnya 2, 3, 5, 7, 11, … bilangan asli yang mempunyai lebih dari dua faktor disebut bilangan komposit (majemuk). Misal 4, 6, 8, 9, …
Teorema : (Topik Erotosthenes)
Untuk setiap bilangan komposit n ada bilangan prima p sehingga p|n dan p .
Teorema di atas
mempunyai makna yang sama dengan “jika tidak ada bilangan prima p yang
dapat membagi n dengan p maka n adalah bilagan prima”.
Contoh soal 4
Tentukan bilangan-bilangan berikut merupakan bilangan prima atau majemuk.
a). 157 b). 221
penyelesaian :
a). Bilangan-bilangan
prima yang adalah 2, 3, 5, 7, 11. Karena tidak ada dari
bilangan-bilangan prima 2, 3, 5, 7, 11 yang dapat dibagi 157, maka 157
merupakan bilangan prima.
b). Bilangan-bilangan prima yang adalah 2, 3, 5, 7, 11, 13. Karena 13|221 maka 221 merupakan bilangan komposit.
Contoh soal 5
Tentukan pasangan-pasangan bilangan asli a dan b sehingga a2 – b2 = 1991.
Penyelesaian :
Karena 1991 merupakan bilangan komposit (1991 = 11 X 181) maka :
A2 – b2 = 1991
(a – b)(a + b) = 1991 (1 X 1991 atau 11 X 181) atau (a – b)(a + b) = 11 X 181
Kemungkinan I Kemungkinan II
a + b = 1991 a + b = 181
a - b = 1 + a – b = 11 +
2a = 1992 2a = 192
a = 996 a = 96
b = 995 b = 85
Jadi pasangan-pasangan bilangan asli a dan b yang memenuhi a2 – b2 = 1991 adalah (996, 995) dan (96, 85)
-
Bilangan kuadrat
Ada tiga hal penting yang perlu duketahui tentang bilangan kuadrat, yaitu :-
Angka satuan yang mungkin untuk bilangan kuadrat adalah 0, 1, 4, 5, 6, dan 9
-
Setiap bilangan kuadrat dibagi 4 maka sisanya 0 atau 1
-
Jika p bilangan prima dan p|n2 maka p2|n2
-
Contoh soal 6
Carilah suatu bilangan kuadrat sempurna yang angka-angkanya berturut-turut adalah :
k, k + 1, k + 2, 3k, k + 3
penyelesaian :
-
Angka pertama adalah k maka k yang mungkin adalah 1, 2, 3, … , 9 ……………………… (1)
-
Angka ketiga adalah 3k maka k yang mungkin adalah 0, 1, 2, 3 …………………………….. (2)Dari (1) dan (2), maka k yang mungkin terjadi 1, 2, 3.
-
Bilangan kuadrat yang mungkin adalah 12334, 233465, 34596.
-
Selanjutnya 12334 dibagi 4 bersisa 2 berarti 12334 bukan bilangan kuadrat.
-
5 karena 4693 tidak lagi dapat dibagi 5 maka 23465 bukan bilangan kuadrat.2 34596 bilangan 334596 = 22 . 32 . 312, berarti 34596 merupakan bilangan kuadrat.2 17298
3 8649
3 2883
31 961
31 31
1
Jadi bilangan kuadrat yang dicari adalah 34596.
-
GCD DAN ALGORITMA EUCLID
Jika a dan b sembarang bilangan bulat dan d bilangan bulat yang memenuhi sifat d|a dan d|b, maka d disebut pembagi persekutuan dari a dan b. Nilai terbesar dari d disebut pembagi persekutuan terbesar Greater Common Divisor (GCD) dan ditulis dengan GCD (a, b)Misal : GCD (8, 12) = 4Pembagi persekutuan terbesar dapat juga ditentukan dengan menggunakan Algoritma Euclede.
Diberikan dua bilangan bulat a dan b dengan a > b > 0, maka GCD (a, b) bisa dicari dengan mengulang algoritma pembagian.
a = q1b + r1 0 < r1 < b
b = q2 r1 + r2 0 < r2 < r1
r1 = q3 r2 + r3 0 < r3 < r2
rn-2 = qn rn-1 + rn 0 < rn-1 < rn-2
rn-1 = qn+1 rn + 0
maka rn , sisa terakhir dari pembagian di atas yang bukan nol merupakan GCD (a, b).
Contoh Soal 7
Tentukan GCD (4840, 1512)
Penyelesaian :
4840 = 3 X 1512 + 304
1512 = 4 X 304 + 296
304 = 1 X 296 + 8
296 = 37 X 8 + 0
Jadi : GCD (4840, 1512) = 8
Jika GCD (a, b) = c maka ada bilangan bulat m dan n sehingga am + bn = c. Mencari m dan n digunakan AlgoritmaEuclede.
Seperti pada contoh soal
7 di dapat bahwa GCD (4840, 1512) = 8, maka ada bilangan bulat m dan n
segingga 4840m + 1512n = 8. Mencari m dan n dimulai dari baris kedua
dari bawah pada Algoritma EucledeI.
8 = 304 – 296
= 304 – (1512 – 4 X 304) = -1512 + 5 X 304
= -1512 + 5 (4840 – 3 X 1512)
8 = 5 X 4840 – 16 X 1512 maka m = 5 dan n = -16
Jika GCD (a, b) = 1 maka a dan b dikatakan saling prima.
Contoh soal 8
Buktikan bahwa jika GCD (a, b) = 1 dan a|bc, maka a|c
Bukti :
Karena GCD (a, b) = 1, maka terdapat bilangan-bilangan m dan n sehingga 1 = ma + nb.
Diketahui a|bc, berarti terdapat bilangan bulat k sehingga bc = ak.
Dengan menggandakan persamaan 1 = ma + nb dengan c didapat :
c = mac + nbc
c = mac + nak
c = a(mc + nk) Û a|c
Contoh soal 9
Jika GCD (a, m) = GCD (b, m) = 1, maka buktikan bahwa GCD (ab, m) = 1.
Bukti :
1 = ax0 + my0
= bx1 + my1
Sehingga : (ax0 + bx1) = (1 – my0)(1 – my1)
= 1 – my1 – my0 + m2y0y1
= 1 – m (y1 + y0 – my0y1)
Tulis : y1 + y0 – my0y1 = y2 , maka :
ab (x0x1) + m(y2) = 1 maka GCD (ab, m) = 1
-
KONGRUEN
Diberikan bilangan bulat n yang lebih besar dari 1 dan bilangan-bilangan bulat a dan b. Bilangan a dikatakan kongruen dengan b modulo n, dituliskan dengan a º b (mod n) jika a dan b memberikan sisa yang sama apabila dibagi oleh n.
Contoh soal 10
Jika a dan b kongruen modulo m, buktikan bahwa selisishnya dapat dibagi m.
Bukti :
a º b (mod m) Þ a = q1m + r dan b = q2m + r
a – b = (q1 – q2)m, akibatnya m | (a – b)
Contoh soal 11
Buktikan bahwa (an + b)m = bm mod (n)
Bukti :
Membuktikan (an + b)m
º bm mod (n) sama artinya dengan membuktikan ada bilangan bulat k sehingga (an + b)m – bm = kn.
º bm mod (n) sama artinya dengan membuktikan ada bilangan bulat k sehingga (an + b)m – bm = kn.
Bukti :
(an + b)m – bm = (an)m + m(an)m-1. b + … + m(an)bm-1 + bm – bm
= {a(an)m-1 + am(an)m-2 + … + am(b)m-1}n
= kn (terbukti )
Rumusan pada contoh nomor 11 di atas dapat digunakan menentukan sisa pembagian bilangan yang cukup benar.
Contoh soal 12
Tentukan angka satuan bilangan 19971991.
Penyelesaian :
Angka satuan 19971991 º sia pembagian 19971991 oleh 10
º (199 X 10 + 7)1991 mod (10)
º 71991 mod (10)
º 74 X 497 + 3 mod (10)
º (74)487 X 73 mod (10)
º (2421)497 X 343 mod (10)
º 1 X 3 mod (10)
º 3 mod (10)
Jadi angka satuan 19971991 adalah 3.
Contoh soal 13
Tentukan sisa jika 319 dibagi oleh 14.
Penyelesaian :
319 mod (14) º 33 X 6 + 1 mod (14)
º (33)6 X 31
mod (14)
mod (14)
º (2 X 14 – 1)6 X 3 mod (14)
º (-1)6 X 3 mod (14)
319 º 3 mod (14)
Jadi sisa pembagian 319 oleh 14 adalah 3.
Contoh soal 14
Tentukan sisa 31990 jika dibagi 41.
Penyelesaian :
31990 m od (41) º 34 X 497 + 2 mod (41)
º (34)497 X 32 mod (41)
º (2 X 41 – 1)497 X 9 mod (41)
º (-1)497 X 9 mod (41)
º -9 mod (41)
º (41 – 9) mod (41)
º 31 mod (41)
Jadi sisa 31990 dinagi oleh 41 adalah 32.
-
PERSAMAAN DIOPHANTINE
Suatu persamaan berbentuk ax + by = c dengan a, b, c bilangan-bilangan bulat dan a, b dua-duanya bukan nol disebut persamaan liner diophantine jika penyelesaiannya dicari untuk bilangan-bilangan bulat.
Teorema :
Persamaan liner
diophantine ax + by = c mempunyai penyelesaian jika dan hanya jika
pembagi persekutuan terbatas dari a dan b membagi c.
Bukti :
Misalkan d = GCD (a, b) dan d|c
d|c Û ada k bulat sehingga c = kd.
d|GCD (a, b) Û ada bilangan bulat m dan n sehingga am + bn = d.
a(km) + b (kn) = kd
a(km) + b (kn) = c
berarti x = mk dan y = nk
Teorema :
Jika d = GCD (a, b) dan x0 , y0 penyelesaian persamaan diophantine ax + by = c, maka penyelesaian umum persamaan tersebut adalah :
x = x0 + dan y = y0 – dengan k parameter bilangan bulat.
Contoh soal 15
Tentukan penyelesaian umum persamaan diophantine 738x + 621y = 45
Penyelesaian :
Mencari GCD (738, 621) dengan Algoritma Euclide.
Mencari GCD (738, 621) dengan Algoritma Euclide.
738 = 1 X 621 + 117
621 = 5 X 117 = 36
117 = 3 X 36 + 9
36 = 4 X 9 + 0
Jadi GCD (738, 621). Karena 9|45 maka persamaan di atas mempunyai penyelesaian.
Menentukan 9 sebagai kombinasi 738 dan 621.
9 = 117 – 3 . 36
= 117 – 3 (621 – 5 X 117) = -3 X 621 + 16 X 117
= -3 X 621 + 16 (738 – 621)
9 = 16 X 738 – 19 X 621
Kalikan kedua ruas dengan 5
45 = 80 X 738 – 45 X 621
Sehingga didapat x0 = 80, y0 = -95
Penyelesaian umumnya adalah :
x = 80 +
x = -95 –
Contoh soal 16
Tentukan x dan y bulat positif yang memenuhi persamaan 7x + 5y = 100
Penyelesaian :
GCD (7, 5) = 1. Karena 1|100 maka persamaan mempunyai penyelesaian.
Dengan mudah bisa ditulis.
1 = 3 . 7 – 4 . 5
100 = 7 X 300 + 5 X (-400). Maka x0 = 300, y0 = -400
Penyelesaian umumnya adalah :
x = 300 + 5k
x = 300 + 5k
Y = -400 – 7k
Karena yang diinginkan penyelesaian positif, maka harus dipenuhi kedua pertidaksamaan :
300 + 5k > 0
-400 – 7k > 0
Yaitu : 60 < k < -57
Jadi persamaan
diophantine 7x + 5y = 100 mempunyai tepat dua penyelesaian positif yaitu
untuk k = -59, dan k = -58 maka x = 5, y = 13 dan untuk k -58 maka x =
10, y = 6.
SOAL LATIHAN BAB III-
Tentukan bilangan empat digit abcd yang memenuhi 4 X (abcd) = dcbaPenyelesaian :
4 X (abcd) = dcba (empat digit), maka nilai a yang mungkin adalah 1 atau 2
4 X (abcd) = … a (beersatuan genap) maka a tidak mungkin 1. Jadi haruslah a = 2. Agar a = 2 maka haruslah d = 8.
32bc84 x8cb2
4 X c + 3 tidak mungkin bersatuan 0 atau 2. Jadi haruslah b = 1
Karena b = 1 maka haruslah c = 7.
Dengan demikian bilangan yang dimaksud adalah 2178.
-
Jika ditulis dalam bilangan basis 10, tentukan banyaknya angka bilangan 416 X 525.Penyelesaian :
416 X 525 = 232 X 525
= 27 X 225 x 525
= 128 X (2 X 5)25
= 128 X 1025
= 1,28 X 1027
Banyaknya angka dari 416 X 525 = 28 angka. -
Tentukan banyaknya angka nol terakhir dari 1000!Penyelesaian :
-
Angka satuan ysng menghasilkan angka nol adalah kelipatan 5 dikali kelipatan 2 yakni sebanyak .
- Angka puluhan yang menghasilkan angka nol sebanyak .
-
Angka ratusan yang menghasilkan angka nol sebanyakJadi banyak angka nol terakhir dari 1000! Adalah 200 + 40 + 8 + 1 = 249
-
Tentukan dua angka terakhir dari bilangan 31234Penyelesaian :
Dua angka terakhir 31234 = sisa pembagian 31234 o leh 100.
31234 mod (100) º (35)206 mod (100)º (243)206 X 34 mod (100)º (43)2 X 103 X 81 mod (100)º (1849)103 X 81 mod (100)º (49)2 X 51 + 1 X 81 mod (100)º (2401)51 X 49 X 81 mod (100)º 151 X 3969 mod (100)º 69 mod (100)Jadi dua angka terakhir dari bilangan 31234 adalah 69. -
Tunjukkan bahwa 3105 + 4105 habis dibagi 7Penyelesaian :
3105 + 4105 mod 97) = 3105 + (7 – 3)105 mod (7)
= 3105 + (-3)105 mod (7)
= 0 mod (7)
Kesimpulan : 3105 + 4105 habis dibagi 7 -
Untuk n bilangan asali, buktikan bahwa n3 + 5n habis dibagi 6.Penyelesaian :
n3 + 5n = n3 – n + 6n
= (n – 1)n (n + 1) + 6n
Karena (n – 1)n (n + 1) merupakan tiga bilangan bulat yang berurutan, maka (n – 1)n (n – 1) habis dibagi 6. Dengan demikian n3 + 5n habis dibagi 6. -
Jika n > 4 merupakan bilangan komposit, maka tunjukkan bahwa n|(n – 1)Penyelesaian :
Karena n bilangan komposit, maka trdapat bilangan bulat n1, n2 sehingga n = n1 n2 dan n1, n2 > 1. Jelas bahwa n1, n2 < n. Dua kasus yang mungkin adalah :
-
n1 = n2, maka kedua bilangan termasuk ke dalam perkalian(n – 1)! = 1, 2 … (n – 1)
Akibatnya n|(n – 1)! -
n1 = n2, maka n = n12. Karena n > 4 maka n1 > 2. Dengan demikian n = n12 = n1 n1 > 2n, hal ini mengakibatkan n1 dan 2n1 kurang dari n masuk ke dalam perkalian(n – 1) | = 1, 2 … (n – 1)
Jadi : 2n12 | (n – 1)! Maka n|(n – 1)!
-
Jika n bilangan bulat, tunjukkan bahwa n4 – 20n2 + 4 bukan bilangan prima.Penyelesaian :
n4 – 20n2 + 4 = n4 – 4n2 + 4 – 16n2
= (n2 – 2)2 – 16n2
= (n2 – 2 – 4n)(n2 – 2 + 4n)
Misalkan : n2- 2 – 4n = 1
n2 – 4n – 3 = 0
n1 . 2 =
Jika n bulat maka n2 – 2 – 4n = 1
Dengan cara yang sama didapat bahwa n2 – 2 – 4n 1 dan n2 – 2 – 4n 1.
Kesimpulan : jika n bulat maka n4 – 20n2 + 4 bukan bilangan prima. -
Jika p > 3 bilangan prima, tunjukkan bahwa 24|p2 – 1Penyelesaian :
Karena p > 3 bilangan prima maka p – 1 dan p + 1 bilangan genap, yang satunya dapat dibagi 2 dan satunya lagi dapat dibagi 4; akibatnya 8|p2 – 1 ……………………………………………….. (1)Sekarang perhatikan bahwa salah satu dari bilangan p – 1, p, p + 1 dapat dibagi 3. Karena p prima yang lebih besar dari 3 maka 3 ł p; akibatnya 3|p2 – 1 ……………………………………… (2)
Karena 3 dan 8 saling prima maka dari (1) dan (2) didapat 24|p2 – 1. -
Buktikan bahwa hanya ada satu nilai n yang membuat 28 + 211 + 2n kuadrat sempurna.Penyelesaian :
Misalkan 28 + 211 + 2n = m2
2n = m2 – 28 (1 + 23)
= m2 – 28 . 9
2n = (m – 48)(m + 48)
Menurut teorema Faktorisasi Tunggal, maka ada bilangan bulat tidak negatif s dan t sehi8ngga ;
M – 48 = 2s. m + 48 = 2t, s + t = n
Jadi :
2s + 48 = 2t – 48
2t – 2s = 96 Þ 2s (2t – s – 1) = 25 X 3
S = 5 dan r = 7
maka n = s + t = 12



 23.45
23.45
 Unknown
Unknown

















 adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan  adalah koordinat pusat lingkaran.
adalah koordinat pusat lingkaran. , maka persamaan di atas dapat dituliskan sebagai
, maka persamaan di atas dapat dituliskan sebagai
 adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan 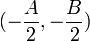 adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.
adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.


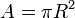


 dan jari-jari luar
dan jari-jari luar 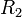 .
.

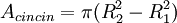
 rumus ini kembali menjadi rumus luas lingkaran.
rumus ini kembali menjadi rumus luas lingkaran.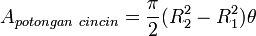
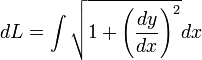
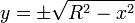
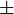 mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan
bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga
sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan
bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga
sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.

 adalah
semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n
unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis
adalah
semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n
unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis  atau
atau  .
.

 .
.








 dibaca “ Kejadian A atau B dan
dibaca “ Kejadian A atau B dan  dibaca “Kejadian A dan B”
dibaca “Kejadian A dan B”
 Jika
Jika  . Sehingga
. Sehingga  Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
Dalam kasus ini, A dan B disebut dua kejadian saling lepas. Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
Dalam kasus ini, dua kejadian tersebut tidak saling bebas.

 dan setiap
dan setiap  maka:
maka:



 untuk n = 0, 1, 2, …. ,n
untuk n = 0, 1, 2, …. ,n




