Integral

Sebuah integral tertentu dari sebuah fungsi dapat digambarkan sebagai area yang dibatasi oleh kurva fungsinya.
Integral adalah sebuah konsep penting dalam
matematika, dan bersama dengan inversnya,
diferensiasi, adalah satu dari dua operasi utama dalam
kalkulus.
Integral ditemukan menyusul ditemukannya masalah dalam diferensiasi di
mana matematikawan harus berpikir bagaimana menyelesaikan masalah yang
berkebalikan dengan solusi diferensiasi. Lambang integral adalah

Bila diberikan suatu
fungsi f dari
variabel real x dengan
interval [a, b] dari sebuah garis lurus, maka
integral tertentu
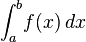
didefinisikan sebagai
area yang dibatasi oleh
kurva f, sumbu-
x, sumbu-
y dan garis vertikal
x = a dan
x = b, dengan area yang berada diatas sumbu-
x bernilai positif dan area dibawah sumbu-
x bernilai negatif.
Kata
integral juga dapat digunakan untuk merujuk pada
antiturunan, sebuah fungsi
F yang turunannya adalah fungsi
f. Pada kasus ini, maka disebut sebagai
integral tak tentu dan notasinya ditulis sebagai:

Prinsip-prinsip dan teknik integrasi dikembangkan terpisah oleh
Isaac Newton dan
Gottfried Leibniz pada akhir abad ke-17. Melalui
teorema fundamental kalkulus yang mereka kembangkan masing-masing, integral terhubung dengan diferensial: jika
f adalah fungsi kontinu yang terdefinisi pada sebuah
interval tertutup [a, b], maka, jika antiturunan
F dari
f diketahui, maka integral tertentu dari
f pada interval tersebut dapat didefinisikan sebagai:
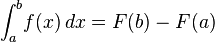
Integral dan diferensial menjadi peranan penting dalam kalkulus, dengan berbagai macam aplikasi pada sains dan
teknik.
Mencari nilai integral
Substitusi
- Contoh soal:
- Cari nilai dari:
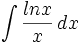




Integrasi parsial
- Integral parsial menggunakan rumus sebagai berikut:
-

- Contoh soal:
- Cari nilai dari:

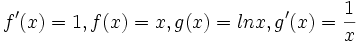
- Gunakan rumus di atas
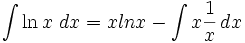
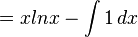

Substitusi trigonometri
- Contoh soal:
- Cari nilai dari:

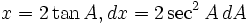





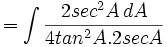
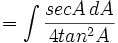

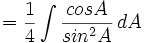
-
-
- Cari nilai dari:
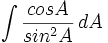 dengan menggunakan substitusi
dengan menggunakan substitusi 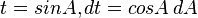
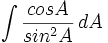
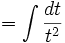
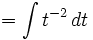
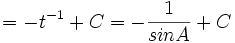
-
- Masukkan nilai tersebut:
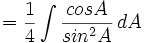
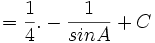

-
- Nilai sin A adalah



Integrasi pecahan parsial
- Contoh soal:
- Cari nilai dari:

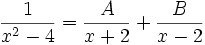

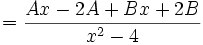
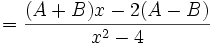
- Akan diperoleh dua persamaan yaitu
 dan
dan 
- Dengan menyelesaikan kedua persamaan akan diperoleh hasil
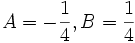
-



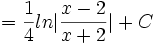
Rumus integrasi dasar
Umum
Bilangan natural

Logaritma

Trigonometri

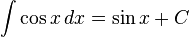
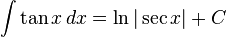
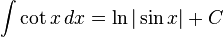


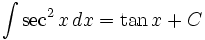

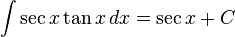


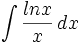

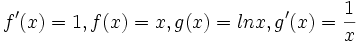
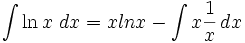
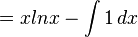




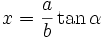



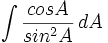 dengan menggunakan substitusi
dengan menggunakan substitusi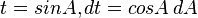
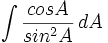
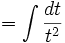
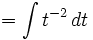
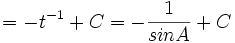
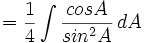
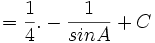





 dan
dan 
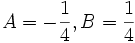
 23.31
23.31
 Unknown
Unknown

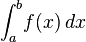

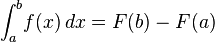





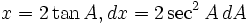




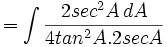
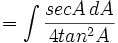

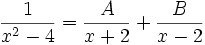

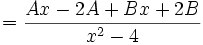
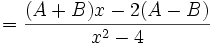


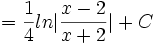



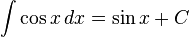
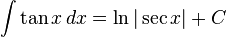
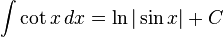


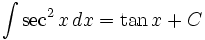

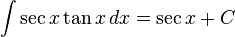

 Posted in
Posted in






0 komentar :
Posting Komentar