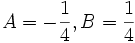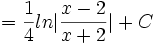SELEKSI OLIMPIADE TINGKAT PROVINSI 2008
TIM OLIMPIADE MATEMATIKA INDONESIA 2009
Prestasi itu diraih bukan didapat !!!
SOLUSI SOAL
Bidang Matematika
Bagian Pertama
Disusun oleh : Eddy Hermanto, ST
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
BAGIAN PERTAMA
1. 2008 = 23 ⋅ 251
Banyaknya pembagi positif dari 2008 = (3 + 1)(1 + 1)
∴ Banyaknya pembagi positif dari 2008 = 8.
2. Banyaknya cara menyusun huruf-huruf MATEMATIKA adalah !2!2!3!10⋅⋅ = 151200
Banyaknya cara menyusun huruf-huruf MATEMATIKA dengan syarat kedua T berdekatan adalah sama dengan banyaknya cara menyusun huruf-huruf MATEMAIKA, yaitu !2!3!9⋅ = 30240
Banyaknya cara menyusun huruf-huruf MATEMATIKA dengan kedua T tidak berdekatan adalah = 151200 − 30240 = 120960.
∴ Banyaknya cara menyusun = 120960.
3. Karena 0 < b < a maka baba−+ akan bernilai positif. 226262222222=−+=−+++=⎟⎠⎞⎜⎝⎛−+abababababbaabbababa
∴ 2=−+baba
4. Misalkan segitiga ABC dimaksud adalah seperti pada gambar berikut
Misalkan juga AC = b
[ABC] = ½ ⋅ AC ⋅ 12 = ½ ⋅ AB ⋅ 4
b ⋅ 12 = AB ⋅ 4
AB = 3b
Misalkan juga BC = a dan panjang garis tinggi dari A adalah x dengan x bilangan asli.
[ABC] = ½ ⋅ a ⋅ x = ½ ⋅ 4 ⋅ 3b
a x = 12b ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (1)
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
Ada dua kemungkinan pemahaman terhadap pertanyaan pada soal. i) Yang ditanyakan adalah maks (x, 4, 12).
Akan dibuktikan bahwa x ≤ 12 sehingga panjang maksimum dari garis tinggi segitiga ABC adalah 12.
Andaikan bahwa x > 12.
Dari persamaan (1) akan didapat bahwa a < b ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (2) Pada segitiga siku-siku ACF jelas bahwa AC = b > AF
Karena AB = 3b maka FB > 2b
Pada segitiga siku-siku BCF berlaku bahwa BC > FB
Karena BC = a < b sedangkan FB > 2b maka ketaksamamaan tidak mungkin terjadi. Kontradiksi dengan pengandaian awal.
Jadi, x ≤ 12.
Maka panjang maksimum garis tinggi segitiga ABC adalah 12.
ii) Yang ditanyakan adalah panjang maksimum dari garis tinggi yang ketiga dari segitiga ABC
• Andaikan 3b adalah sisi terpanjang
Berdasarkan ketaksamaan segitiga berlaku
3b < a + b
Maka 2b < a
Berdasarkan persamaan (1) maka
a x < 6a
Jadi, x < 6
* Jika x = 5 maka a = 512b
AC2 + BC2 = 22225169512bbb=⎟⎠⎞⎜⎝⎛+ < AB2
Jadi, jika x = 5 maka segitiga BC tumpul. Tidak memenuhi bahwa segitiga ABC lancip.
* Jika x = 4 maka a = 3b
Segitiga ABC sama kaki dengan BC = AB = 3b
Karena AB adalah sisi terpanjang maka segitiga BC lancip.
• Andaikan a adalah sisi terpanjang
3b < a
xa = 12b < 4a
x < 4
Karena x ≤ 4 maka tidak perlu lagi mencari nilai x maksimum.
Jadi, panjang maksimum garis tinggi yang ketiga dari segitiga ABC adalah 4.
∴ Dari dua kemungkinan ini Penulis lebih cenderung pada kemungkinan pertama yang sesua dengan kata-kata pada soal. Panjang maksimum garis tinggi dari segitiga ABC adalah 12.
5. Misalkan persamaan garis tersebut adalah y = mx + c
Misalkan juga garis memotong sumbu X di (p, 0) dan sumbu Y di (0, q) dengan p adalah bilangan prima dan q adalah bilangan bulat positif.
Karena garis memotong sumbu X di (p, 0) dan sumbu Y di (0, q) maka persamaan garis tersebut adalah cxpqy+−=.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
Garis melalui (0, q) maka c = q. Jadi persamaan garis tersebut adalah qxpqy+−=
Karena garis melalui (4, 3) maka berlaku
3p = −4q + pq
(p − 4)(q − 3) = 12
* Jika p genap maka p = 2 sehingga q = −3. Tidak memenuhi q bulat positif.
* Jika p ganjil maka p − 4 ganjil. Nilai p − 4 yang mungkin memenuhi adalah ±1 atau ±3.
- Jika p − 4 = −1 maka p = 3 dan q = −9. Tidak memenuhi q bulat positif.
- Jika p − 4 = 1 maka p = 5 dan q = 15. Jadi persamaan garis adalah y = −3x + 15 yang melalui titik (4, 3)
- Jika p − 4 = −3 maka p = 1 yang tidak memenuhi bahwa p adalah bilangan prima.
- Jika p − 4 = 3 maka p = 7 dan q = 7. Jadi persamaan garis adalah y = −x + 7 yang melalui titik (4, 3)
Persamaan garis yang memenuhi adalah y = −3x + 15 dan y = −x + 7.
∴ Banyaknya garis yang memenuhi ada 2.
6. Perhatikan gambar. Diketahui dari soal ∠BAC = 45o.
Misalkan luas segitiga ABC = [ABC]
Dengan dalil pitagoras didapat :
AC2 = AD2 + 4 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (1)
AB2 = AD2 + 9 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (2)
Persamaan (2) jumlahkan dengan (1) didapat
AB2 + AC2 = 2AD2 + 13 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (3)
[ABC] = ½ BC ⋅ AD
Karena BC = 5 maka AD = []52ABC ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (4)
Pada segitiga ABC berlaku
BC2 = AB2 + AC2 − 2 AB AC cos 45o = AB2 + AC2 − 2 AB AC sin 45o
25 = 2 AD2 + 13 − 4[ABC] ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (5)
Subtitusikan persamaan (4) ke (5)
[][]ABCABC4258122−=
(2[ABC] + 5)([ABC] − 15) = 0
Maka [ABC] = 15
∴ Luas segitiga ABC adalah 15.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
7. Persamaan tersebut dapat diubah menjadi (3x2 + 1)(y2 − 10) = 507 = 3 ⋅ 132
Karena 3x2 + 1 bulat positif maka y2 − 10 juga bilangan bulat positif. Faktor positif dari 507 ada 6 yaitu 1, 3, 13, 39, 169 dan 507.
y2 − 10 adalah faktor dari 507 maka y2 = 11, 13, 23, 49, 179 atau 517 dan yang merupakan bilangan kuadrat sempurna hanya 49. Maka y2 = 49.
Sehingga 3x2 + 1 = 13.
∴ 3x2y2 = 12 x 49 = 588.
8. ()°°+°−°=°−°=°30tan45tan130tan45tan3045tan15tan 3333333333111331115tan++⋅+−=⋅+−=° 323315tan+=° ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (1)
Dengan dalil cosinus BbAa∠=∠sinsin sehingga 32sinsin+==∠∠baBA ()BA∠+=∠sin32sin ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (2)
Karena ∠C = 60o maka ∠A = 120o − ∠B
sin ∠A = sin (120o − ∠B) = sin 120o cos ∠B − cos 120o sin ∠B ()BBB∠+∠=∠+sin21cos321sin32 BB∠=∠⎟⎠⎞⎜⎝⎛+cos321sin323 oB15tan3233tan=+=∠
∴ Besarnya sudut B adalah 15o.
9. Karena banyaknya siswa = 100 orang sedangkan banyaknya siswa kelas II 50% lebih banyak dari siswa kelas III maka banyaknya siswa kelas II yang mengikuti seleksi = 60 orang sedangkan siswa kelas III = 40 orang.
Misalkan skor rata-rata kelas III adalah x maka skor rata-rata kelas II adalah 32x. 100403260100xx⋅+⋅=
x = 125
∴ Skor rata-rata siswa kelas III adalah 125.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
10. Misalkan panjang AD = x dan panjang AE = y
Luas ΔABC = 21(5)(12) = 30 dan sin A = 135 serta cos A = 1312
Luas ΔADE = 21xy sin A = 15. Maka xy = 78.
Sesuai dalil cosinus pada ΔADE maka :
DE2 = x2 + y2 − 2xy cos A = x2 + y2 − 144
Dengan AM-GM maka
DE2 ≥ 2xy − 144 = 12
DE2 akan minimum sama dengan 12 jika x = y = 78
∴ DEminimum = 32
11. Misalkan ke-4 akar tersebut adalah x1, x2, x3 dan x4 dengan x1 = 2 dan x2 = 2008 = 5022.
x4 + ax3 + bx2 + cx + d = (x − x1) (x − x2) (x − x3) (x − x4) = 0
x1 + x2 + x3 + x4 = −a yang merupakan bilangan rasional. Maka ada 2 kemungkinan nilai x3 dan x4.
• x3 = p − 2 − 5022 dan x4 = q untuk p dan q bilangan rasional.
x1x2x
3
x4 = d yang merupakan bilangan rasional. ( 2)(2 502 )(p − 2 − 2 502 )(q) = bilangan rasional untuk p, q rasional
4 p 251 − 4 251 − 2008 2 = bilangan rasional.
Maka tidak ada p rasional yang memenuhi
• x3 = p − 2 dan x4 = q − 5022 untuk p dan q bilangan rasional.
x1x2x
3
x4 = d yang merupakan bilangan rasional. ( 2)(2 502 )(p − 2)(q − 2 502 ) = bilangan rasional
4 pq 251 − 2008 p 2 − 4q 502 + 4016 = bilangan rasional
Kesamaan di atas akan terpenuhi hanya jika p = q = 0 sehingga x3 = −2 dan x4 = −2008
x4 + ax3 + bx2 + cx + d = (x − 2) (x − 2008) (x + 2) (x + 2008)
x4 + ax3 + bx2 + cx + d = (x2 − 2)(x2 − 2008) = x4 − 2010x2 + 4016
Maka a = 0, b = −2010, c = 0 dan d = 4016
a + b + c + d = 0 − 2010 + 0 + 4016
∴ Nilai a + b + c + d adalah 2006.
12. Misalkan [ABC] menyatakan luas ΔABC.
Berdasarkan dalil cosinus, cos ∠A = ACABBCACAB⋅⋅−+2222.
Maka ctg ∠A = AA∠∠sincos = AACABBCACAB∠⋅⋅⋅−+sin2222 = []ABCBCACAB4222−+
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
Dengan cara yang sama didapat :
ctg ∠B = []ABCACBCAB4222−+ dan ctg ∠C = []ABCABBCAC4222−+
ctg ∠A + ctg ∠B + ctg ∠C = []ABCBCACAB4222++ = 416
∴ ctg ∠A + ctg ∠B + ctg ∠C = 4.
13. f(x) = x2 + 4
f(xy) = x2y2 + 4
f(y − x) = (y − x)2 + 4
f(y + x) = (y + x)2 + 4
f(xy) + f(y − x) = f(y + x)
x2y2 + 4 + (y − x)2 + 4 = (y + x)2 + 4
x2y2 + y2 + x2 − 2xy + 4 = y2 + x2 + 2xy
x2y2 + 4 = 4xy
(xy − 2)2 = 0
Jadi xy = 2
Dengan ketaksamaan AM-GM maka 222=≥+xyyx
∴ Nilai minimum dari x + y adalah 22
14. Jelas bahwa n harus genap.
Misalkan n = 2y ⋅ p1x1 ⋅ p2x2 ⋅ ⋅⋅⋅ ⋅ pkxk dengan pi untuk i = 1, 2, ⋅⋅⋅, k semuanya bilangan prima ganjil dan xi untuk i = i, 2, ⋅⋅⋅, k semuanya bilangan bulat tak negatif serta y asli.
Karena salah satu faktor dari n adalah 2 maka semua bilangan genap ≤ n tidak akan relatif prima dengan n. Banyaknya bilangan genap ≤ n ada tepat sebanyak 2n dan banyaknya bilangan ganjil kurang dari n juga ada sebanyak 2n.
Tetapi untuk semua 1 < pi < n dengan i = 1, 2, ⋅⋅⋅, k juga merupakan faktor dari n yang mengakibatkan semua 1 < pi < n dengan i = 1, 2, ⋅⋅⋅, k tidak akan relatif prima dengan n.
Maka agar terpenuhi ada tepat 2n bilangan kurang dari n dan relatif prima terhadap n maka n tidak boleh memiliki faktor ganjil selain 1. Jadi pi = 1 untuk semua i = 1, 2, ⋅⋅⋅, k.
Maka n = 2y untuk suatu bilangan asli y.
Karena n < 2008 maka 2y < 2008. Jadi y ≤ 10.
Maka nilai n yang memenuhi adalah 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024.
∴ Banyaknya bilangan bulat positif n yang memenuhi ada 10.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
15. Misalkan f(x) berderajat n maka f(x2) akan berderajat 2n.
x3f(x) akan berderajat n + 3.
• Jika n > 3 maka 2n > n + 3 sehingga f(x2) − x3f(x) akan berderajat 2n > 6. Jadi, tanda kesamaan tidak mungkin terjadi.
• Jika n = 3 maka f(x2) dan x3f(x) akan berderajat sama yaitu 6 sehingga masih dimungkinkan f(x2) − x3f(x) akan berderajat 3.
Jika f(x) = x3 − 2 maka f(x2) − x3f(x) = (x6 − 2) − x3(x3 − 2) = 2(x3 − 1) yang memenuhi.
• Jika n < 3 maka 2n < n + 3 sehingga f(x2) − x3f(x) akan berderajat n + 3. Karena ruas kanan berderajat 3 maka n = 0.
∴ Derajat f(x) adalah 3.
16. Banyaknya cara memilih 2 orang dari 20 orang = 20C2 = 190.
Banyaknya kemungkinan tanggal lahir dari 20 orang = 36520.
Peluang = 202203651347363364365⋅⋅⋅⋅⋅⋅LC
∴ Peluang dari soal = 20365!346!365190⋅⋅dengan tanda “!” menyatakan faktorial.
17. Ada dua kemungkinan jumlah ketiga bilangan tersebut genap
• Ketiga bilangan tersebut semuanya genap
Peluang = 1338167620062007200861002100310043200831004=⋅⋅⋅⋅=CC
• Ada satu bilangan genap dan dua lainnya ganjil 133850262006200720082100310041004320082100411004=⋅⋅⋅⋅=⋅CCC
Peluang jumlah ketiga bilangan tersebut genap = 13385021338167+
∴ Peluang jumlah ketiga bilangan tersebut genap = 21
18. ⏐A ∪ B⏐ = ⏐A⏐ + ⏐B⏐ − ⏐A ∩ B⏐
10 = 4 + ⏐B⏐ − ⏐A ∩ B⏐
⏐B⏐ − ⏐A ∩ B⏐ = 6
Jelas bahwa 0 ≤ ⏐A ∩ B⏐ ≤ ⏐A⏐ sehingga 0 ≤ ⏐A ∩ B⏐ ≤ 4.
Jadi 6 ≤ ⏐B⏐ ≤ 10
Karena ⏐B⏐ bulat tak negatif maka ⏐B⏐ = 6, 7, 8, 9 atau 10.
∴ ⏐B⏐ = 6, 7, 8, 9 atau 10.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
19. Misalkan ∠DAB = ∠ACD = α
ctg α = ADCDBDAD= 686CD= sehingga CD = 29
Luas segitiga ABC = ½ ⋅ (BD + CD) ⋅ AD = 275
∴ Luas segitiga ABC = 275
20. Dengan binom Newton didapat
()Σ=⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛=+=1004010042101004100410043310041004321004311004301004134kkkL
∴ = 2Σ=⎟⎟⎠⎞⎜⎜⎝⎛1004010043kkk2008.
TIM OLIMPIADE MATEMATIKA INDONESIA 2009
Prestasi itu diraih bukan didapat !!!
SOLUSI SOAL
Bidang Matematika
Bagian Pertama
Disusun oleh : Eddy Hermanto, ST
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
BAGIAN PERTAMA
1. 2008 = 23 ⋅ 251
Banyaknya pembagi positif dari 2008 = (3 + 1)(1 + 1)
∴ Banyaknya pembagi positif dari 2008 = 8.
2. Banyaknya cara menyusun huruf-huruf MATEMATIKA adalah !2!2!3!10⋅⋅ = 151200
Banyaknya cara menyusun huruf-huruf MATEMATIKA dengan syarat kedua T berdekatan adalah sama dengan banyaknya cara menyusun huruf-huruf MATEMAIKA, yaitu !2!3!9⋅ = 30240
Banyaknya cara menyusun huruf-huruf MATEMATIKA dengan kedua T tidak berdekatan adalah = 151200 − 30240 = 120960.
∴ Banyaknya cara menyusun = 120960.
3. Karena 0 < b < a maka baba−+ akan bernilai positif. 226262222222=−+=−+++=⎟⎠⎞⎜⎝⎛−+abababababbaabbababa
∴ 2=−+baba
4. Misalkan segitiga ABC dimaksud adalah seperti pada gambar berikut
Misalkan juga AC = b
[ABC] = ½ ⋅ AC ⋅ 12 = ½ ⋅ AB ⋅ 4
b ⋅ 12 = AB ⋅ 4
AB = 3b
Misalkan juga BC = a dan panjang garis tinggi dari A adalah x dengan x bilangan asli.
[ABC] = ½ ⋅ a ⋅ x = ½ ⋅ 4 ⋅ 3b
a x = 12b ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (1)
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
Ada dua kemungkinan pemahaman terhadap pertanyaan pada soal. i) Yang ditanyakan adalah maks (x, 4, 12).
Akan dibuktikan bahwa x ≤ 12 sehingga panjang maksimum dari garis tinggi segitiga ABC adalah 12.
Andaikan bahwa x > 12.
Dari persamaan (1) akan didapat bahwa a < b ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (2) Pada segitiga siku-siku ACF jelas bahwa AC = b > AF
Karena AB = 3b maka FB > 2b
Pada segitiga siku-siku BCF berlaku bahwa BC > FB
Karena BC = a < b sedangkan FB > 2b maka ketaksamamaan tidak mungkin terjadi. Kontradiksi dengan pengandaian awal.
Jadi, x ≤ 12.
Maka panjang maksimum garis tinggi segitiga ABC adalah 12.
ii) Yang ditanyakan adalah panjang maksimum dari garis tinggi yang ketiga dari segitiga ABC
• Andaikan 3b adalah sisi terpanjang
Berdasarkan ketaksamaan segitiga berlaku
3b < a + b
Maka 2b < a
Berdasarkan persamaan (1) maka
a x < 6a
Jadi, x < 6
* Jika x = 5 maka a = 512b
AC2 + BC2 = 22225169512bbb=⎟⎠⎞⎜⎝⎛+ < AB2
Jadi, jika x = 5 maka segitiga BC tumpul. Tidak memenuhi bahwa segitiga ABC lancip.
* Jika x = 4 maka a = 3b
Segitiga ABC sama kaki dengan BC = AB = 3b
Karena AB adalah sisi terpanjang maka segitiga BC lancip.
• Andaikan a adalah sisi terpanjang
3b < a
xa = 12b < 4a
x < 4
Karena x ≤ 4 maka tidak perlu lagi mencari nilai x maksimum.
Jadi, panjang maksimum garis tinggi yang ketiga dari segitiga ABC adalah 4.
∴ Dari dua kemungkinan ini Penulis lebih cenderung pada kemungkinan pertama yang sesua dengan kata-kata pada soal. Panjang maksimum garis tinggi dari segitiga ABC adalah 12.
5. Misalkan persamaan garis tersebut adalah y = mx + c
Misalkan juga garis memotong sumbu X di (p, 0) dan sumbu Y di (0, q) dengan p adalah bilangan prima dan q adalah bilangan bulat positif.
Karena garis memotong sumbu X di (p, 0) dan sumbu Y di (0, q) maka persamaan garis tersebut adalah cxpqy+−=.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
Garis melalui (0, q) maka c = q. Jadi persamaan garis tersebut adalah qxpqy+−=
Karena garis melalui (4, 3) maka berlaku
3p = −4q + pq
(p − 4)(q − 3) = 12
* Jika p genap maka p = 2 sehingga q = −3. Tidak memenuhi q bulat positif.
* Jika p ganjil maka p − 4 ganjil. Nilai p − 4 yang mungkin memenuhi adalah ±1 atau ±3.
- Jika p − 4 = −1 maka p = 3 dan q = −9. Tidak memenuhi q bulat positif.
- Jika p − 4 = 1 maka p = 5 dan q = 15. Jadi persamaan garis adalah y = −3x + 15 yang melalui titik (4, 3)
- Jika p − 4 = −3 maka p = 1 yang tidak memenuhi bahwa p adalah bilangan prima.
- Jika p − 4 = 3 maka p = 7 dan q = 7. Jadi persamaan garis adalah y = −x + 7 yang melalui titik (4, 3)
Persamaan garis yang memenuhi adalah y = −3x + 15 dan y = −x + 7.
∴ Banyaknya garis yang memenuhi ada 2.
6. Perhatikan gambar. Diketahui dari soal ∠BAC = 45o.
Misalkan luas segitiga ABC = [ABC]
Dengan dalil pitagoras didapat :
AC2 = AD2 + 4 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (1)
AB2 = AD2 + 9 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (2)
Persamaan (2) jumlahkan dengan (1) didapat
AB2 + AC2 = 2AD2 + 13 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (3)
[ABC] = ½ BC ⋅ AD
Karena BC = 5 maka AD = []52ABC ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (4)
Pada segitiga ABC berlaku
BC2 = AB2 + AC2 − 2 AB AC cos 45o = AB2 + AC2 − 2 AB AC sin 45o
25 = 2 AD2 + 13 − 4[ABC] ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (5)
Subtitusikan persamaan (4) ke (5)
[][]ABCABC4258122−=
(2[ABC] + 5)([ABC] − 15) = 0
Maka [ABC] = 15
∴ Luas segitiga ABC adalah 15.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
7. Persamaan tersebut dapat diubah menjadi (3x2 + 1)(y2 − 10) = 507 = 3 ⋅ 132
Karena 3x2 + 1 bulat positif maka y2 − 10 juga bilangan bulat positif. Faktor positif dari 507 ada 6 yaitu 1, 3, 13, 39, 169 dan 507.
y2 − 10 adalah faktor dari 507 maka y2 = 11, 13, 23, 49, 179 atau 517 dan yang merupakan bilangan kuadrat sempurna hanya 49. Maka y2 = 49.
Sehingga 3x2 + 1 = 13.
∴ 3x2y2 = 12 x 49 = 588.
8. ()°°+°−°=°−°=°30tan45tan130tan45tan3045tan15tan 3333333333111331115tan++⋅+−=⋅+−=° 323315tan+=° ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (1)
Dengan dalil cosinus BbAa∠=∠sinsin sehingga 32sinsin+==∠∠baBA ()BA∠+=∠sin32sin ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (2)
Karena ∠C = 60o maka ∠A = 120o − ∠B
sin ∠A = sin (120o − ∠B) = sin 120o cos ∠B − cos 120o sin ∠B ()BBB∠+∠=∠+sin21cos321sin32 BB∠=∠⎟⎠⎞⎜⎝⎛+cos321sin323 oB15tan3233tan=+=∠
∴ Besarnya sudut B adalah 15o.
9. Karena banyaknya siswa = 100 orang sedangkan banyaknya siswa kelas II 50% lebih banyak dari siswa kelas III maka banyaknya siswa kelas II yang mengikuti seleksi = 60 orang sedangkan siswa kelas III = 40 orang.
Misalkan skor rata-rata kelas III adalah x maka skor rata-rata kelas II adalah 32x. 100403260100xx⋅+⋅=
x = 125
∴ Skor rata-rata siswa kelas III adalah 125.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
10. Misalkan panjang AD = x dan panjang AE = y
Luas ΔABC = 21(5)(12) = 30 dan sin A = 135 serta cos A = 1312
Luas ΔADE = 21xy sin A = 15. Maka xy = 78.
Sesuai dalil cosinus pada ΔADE maka :
DE2 = x2 + y2 − 2xy cos A = x2 + y2 − 144
Dengan AM-GM maka
DE2 ≥ 2xy − 144 = 12
DE2 akan minimum sama dengan 12 jika x = y = 78
∴ DEminimum = 32
11. Misalkan ke-4 akar tersebut adalah x1, x2, x3 dan x4 dengan x1 = 2 dan x2 = 2008 = 5022.
x4 + ax3 + bx2 + cx + d = (x − x1) (x − x2) (x − x3) (x − x4) = 0
x1 + x2 + x3 + x4 = −a yang merupakan bilangan rasional. Maka ada 2 kemungkinan nilai x3 dan x4.
• x3 = p − 2 − 5022 dan x4 = q untuk p dan q bilangan rasional.
x1x2x
3
x4 = d yang merupakan bilangan rasional. ( 2)(2 502 )(p − 2 − 2 502 )(q) = bilangan rasional untuk p, q rasional
4 p 251 − 4 251 − 2008 2 = bilangan rasional.
Maka tidak ada p rasional yang memenuhi
• x3 = p − 2 dan x4 = q − 5022 untuk p dan q bilangan rasional.
x1x2x
3
x4 = d yang merupakan bilangan rasional. ( 2)(2 502 )(p − 2)(q − 2 502 ) = bilangan rasional
4 pq 251 − 2008 p 2 − 4q 502 + 4016 = bilangan rasional
Kesamaan di atas akan terpenuhi hanya jika p = q = 0 sehingga x3 = −2 dan x4 = −2008
x4 + ax3 + bx2 + cx + d = (x − 2) (x − 2008) (x + 2) (x + 2008)
x4 + ax3 + bx2 + cx + d = (x2 − 2)(x2 − 2008) = x4 − 2010x2 + 4016
Maka a = 0, b = −2010, c = 0 dan d = 4016
a + b + c + d = 0 − 2010 + 0 + 4016
∴ Nilai a + b + c + d adalah 2006.
12. Misalkan [ABC] menyatakan luas ΔABC.
Berdasarkan dalil cosinus, cos ∠A = ACABBCACAB⋅⋅−+2222.
Maka ctg ∠A = AA∠∠sincos = AACABBCACAB∠⋅⋅⋅−+sin2222 = []ABCBCACAB4222−+
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
Dengan cara yang sama didapat :
ctg ∠B = []ABCACBCAB4222−+ dan ctg ∠C = []ABCABBCAC4222−+
ctg ∠A + ctg ∠B + ctg ∠C = []ABCBCACAB4222++ = 416
∴ ctg ∠A + ctg ∠B + ctg ∠C = 4.
13. f(x) = x2 + 4
f(xy) = x2y2 + 4
f(y − x) = (y − x)2 + 4
f(y + x) = (y + x)2 + 4
f(xy) + f(y − x) = f(y + x)
x2y2 + 4 + (y − x)2 + 4 = (y + x)2 + 4
x2y2 + y2 + x2 − 2xy + 4 = y2 + x2 + 2xy
x2y2 + 4 = 4xy
(xy − 2)2 = 0
Jadi xy = 2
Dengan ketaksamaan AM-GM maka 222=≥+xyyx
∴ Nilai minimum dari x + y adalah 22
14. Jelas bahwa n harus genap.
Misalkan n = 2y ⋅ p1x1 ⋅ p2x2 ⋅ ⋅⋅⋅ ⋅ pkxk dengan pi untuk i = 1, 2, ⋅⋅⋅, k semuanya bilangan prima ganjil dan xi untuk i = i, 2, ⋅⋅⋅, k semuanya bilangan bulat tak negatif serta y asli.
Karena salah satu faktor dari n adalah 2 maka semua bilangan genap ≤ n tidak akan relatif prima dengan n. Banyaknya bilangan genap ≤ n ada tepat sebanyak 2n dan banyaknya bilangan ganjil kurang dari n juga ada sebanyak 2n.
Tetapi untuk semua 1 < pi < n dengan i = 1, 2, ⋅⋅⋅, k juga merupakan faktor dari n yang mengakibatkan semua 1 < pi < n dengan i = 1, 2, ⋅⋅⋅, k tidak akan relatif prima dengan n.
Maka agar terpenuhi ada tepat 2n bilangan kurang dari n dan relatif prima terhadap n maka n tidak boleh memiliki faktor ganjil selain 1. Jadi pi = 1 untuk semua i = 1, 2, ⋅⋅⋅, k.
Maka n = 2y untuk suatu bilangan asli y.
Karena n < 2008 maka 2y < 2008. Jadi y ≤ 10.
Maka nilai n yang memenuhi adalah 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024.
∴ Banyaknya bilangan bulat positif n yang memenuhi ada 10.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
15. Misalkan f(x) berderajat n maka f(x2) akan berderajat 2n.
x3f(x) akan berderajat n + 3.
• Jika n > 3 maka 2n > n + 3 sehingga f(x2) − x3f(x) akan berderajat 2n > 6. Jadi, tanda kesamaan tidak mungkin terjadi.
• Jika n = 3 maka f(x2) dan x3f(x) akan berderajat sama yaitu 6 sehingga masih dimungkinkan f(x2) − x3f(x) akan berderajat 3.
Jika f(x) = x3 − 2 maka f(x2) − x3f(x) = (x6 − 2) − x3(x3 − 2) = 2(x3 − 1) yang memenuhi.
• Jika n < 3 maka 2n < n + 3 sehingga f(x2) − x3f(x) akan berderajat n + 3. Karena ruas kanan berderajat 3 maka n = 0.
∴ Derajat f(x) adalah 3.
16. Banyaknya cara memilih 2 orang dari 20 orang = 20C2 = 190.
Banyaknya kemungkinan tanggal lahir dari 20 orang = 36520.
Peluang = 202203651347363364365⋅⋅⋅⋅⋅⋅LC
∴ Peluang dari soal = 20365!346!365190⋅⋅dengan tanda “!” menyatakan faktorial.
17. Ada dua kemungkinan jumlah ketiga bilangan tersebut genap
• Ketiga bilangan tersebut semuanya genap
Peluang = 1338167620062007200861002100310043200831004=⋅⋅⋅⋅=CC
• Ada satu bilangan genap dan dua lainnya ganjil 133850262006200720082100310041004320082100411004=⋅⋅⋅⋅=⋅CCC
Peluang jumlah ketiga bilangan tersebut genap = 13385021338167+
∴ Peluang jumlah ketiga bilangan tersebut genap = 21
18. ⏐A ∪ B⏐ = ⏐A⏐ + ⏐B⏐ − ⏐A ∩ B⏐
10 = 4 + ⏐B⏐ − ⏐A ∩ B⏐
⏐B⏐ − ⏐A ∩ B⏐ = 6
Jelas bahwa 0 ≤ ⏐A ∩ B⏐ ≤ ⏐A⏐ sehingga 0 ≤ ⏐A ∩ B⏐ ≤ 4.
Jadi 6 ≤ ⏐B⏐ ≤ 10
Karena ⏐B⏐ bulat tak negatif maka ⏐B⏐ = 6, 7, 8, 9 atau 10.
∴ ⏐B⏐ = 6, 7, 8, 9 atau 10.
Solusi Olimpiade Matematika Tk Provinsi 2008 Bagian Kedua
SMA Negeri 5 Bengkulu Eddy Hermanto, ST
19. Misalkan ∠DAB = ∠ACD = α
ctg α = ADCDBDAD= 686CD= sehingga CD = 29
Luas segitiga ABC = ½ ⋅ (BD + CD) ⋅ AD = 275
∴ Luas segitiga ABC = 275
20. Dengan binom Newton didapat
()Σ=⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛=+=1004010042101004100410043310041004321004311004301004134kkkL
∴ = 2Σ=⎟⎟⎠⎞⎜⎜⎝⎛1004010043kkk2008.



 18.59
18.59
 Unknown
Unknown








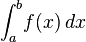

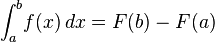
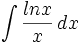






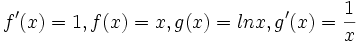
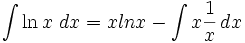
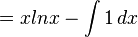




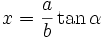



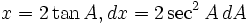




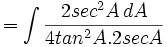
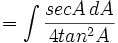

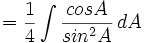
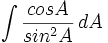 dengan menggunakan substitusi
dengan menggunakan substitusi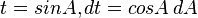
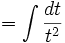
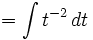
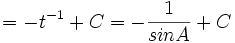
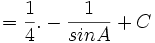




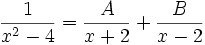

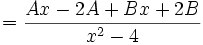
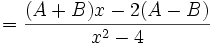
 dan
dan